Stubs (I)
¿Cuándo tenemos que preocuparnos por ellos? Una aproximación al asunto en el dominio de la frecuencia

Definición
Una definición informal de un stub1 podría ser “una línea de transmisión que no está en el camino de la señal”. Fifémoslo en la memoria.
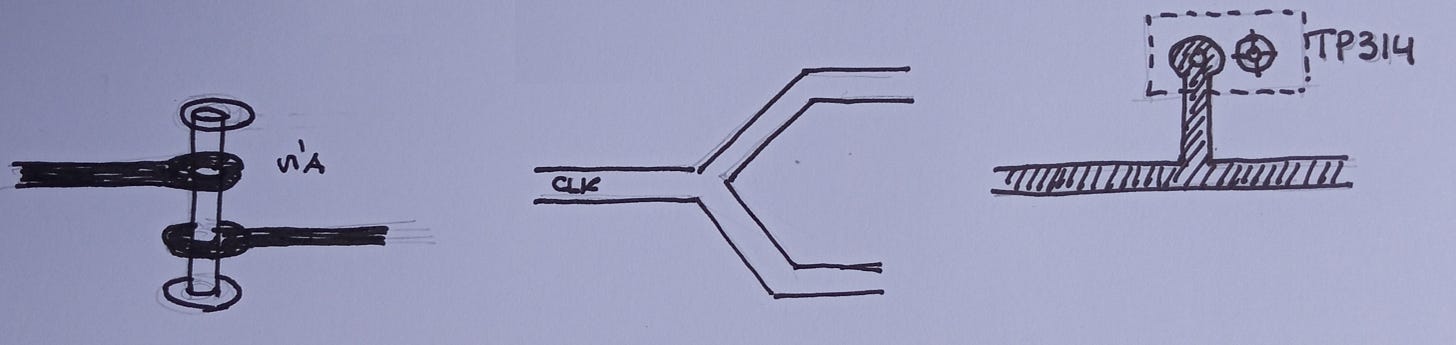
Algunos ejemplos de posibles stubs son:
Trazas en forma de Y
Puntos de prueba
Terminaciones pasivas
Vías en PCB
Me refiero a ‘posibles stubs’ su efecto puede ser completamente ignorado dependiendo del ancho de banda de la señal. Por ejemplo, una vía que atraviesa el circuito impreso de lado a lado puede ignorarse por completo en la mayoría de las aplicaciones, pero puede ser un problema en un sistema PCIe Gen3 (8 Gbps).
Los efectos de un stub
Echemos un vistazo a la siguiente figura. En ella tenemos dos líneas de transmisión, pero existe una tercera que no está en el camino de la señal y que está sin terminar. [Si la terminación sería perfecta no habría reflexiones y la historia sería otra].
En este sistema tenemos dos señales:
La directa (en color azul),
La que viaja a través del stub, se refleja y se mezcla con la directa (dibujada en color rojo). Obsérvese que el dibujo es una simplificación, ya que habrá reflexiones en cada discontinuidad y estas reflexiones se propagan en ambas direcciones. Sin embargo, es una simplificación muy útil para comprender lo que ocurre.
En el mensaje de hoy vamos a hacer un análisis en el dominio de la frecuencia para ganar visión del efecto del stub.
Imaginemos que el stub está completamente abierto en su terminación. No circulará corriente a tierra y, por tanto, la señal incidente se reflejará con la misma forma de onda y aparecerá en el punto de unión con la misma amplitud y un retardo. A cierta frecuencia, el retardo de ida y vuelta del stub será de medio ciclo y la señal retardada se combinará con la onda incidente, produciendo una señal nula: una hachazo (notch) en la respuesta en frecuencia. Lo mismo ocurrirá cuando el retardo sea de un periodo y medio. Tendremos un comportamiento periódico de nulos.
Si el stub no es exactamente un circuito abierto (una carga capacitiva es muy habitual), la reflexión no será perfecta y la respuesta en frecuencia del circuito no será una hachazo ideal (atenuación infinita), sino de un grado variable de intensidad. Lo mismo ocurrirá si las pérdidas en la línea de transmisión del stub son importantes: habrá algo de rizado, atenuación extra a estas frecuencias.
Utilicemos LTspice para hacer algunas simulaciones interesantes. En el siguiente sistema tenemos:
Un generador de tensión configurado para hacer un barrido de frecuencia.
Un divisor de tensión. Podríamos utilizar líneas de transmisión pero complicaría bastante la comprensión del funcionamiento del stub.
Una línea de transmisión terminada en tres posibles valores de condensador porque la terminación capacitiva (parásita) de un stub es bastante habitual.
El stub está definido como una línea de transmisión con un valor de retardo arbitrario de 5 ns. La frecuencia del notch será aquella en la que el retardo de ida y vuelta en el stub sea igual a un semiperiodo: aquella en la que la señal reflejada está en antifase de la onda incidente. Dicho de otro modo: el notch será en la frecuencia en la que el retardo del stub sea un cuarto del periodo de la señal. Esta es la razón por la que a veces hablamos de la frecuencia de cuarto de longitud de onda del stub. El notch se produce en la frecuencia de un cuarto de onda y en todos sus múltiplos impares.
En la simulación se ha incluido tres posibles valores del condensador de terminación:
0,1 pF, que es muy similar a un circuito abierto puro: vemos que el stub produce un notch muy profundo a 50 MHz.
1 pF, que es una carga muy ligera que produce un pequeño desplazamiento en la frecuencia del notch y una atenuación levemente menos profunda.
10 pF, que produce un cambio pequeño pero no despreciable en el retardo de la línea (como veremos en un próximo post) y por tanto reduce la frecuencia de resonancia. Notch menos profundo.
El efecto de un stub es un rizado en la respuesta en frecuencia del sistema.
Como caso particular, un stub sin terminar produce notches en la respuesta en frecuencia.
Como regla general, el efecto de un stub puede despreciarse para frecuencias inferiores a la mitad de la frecuencia del notch.
Merece la pena fijarse en la magnitud del notch. ¡El retardo de 5 ns es el que obtenemos de 1 m de cable RG58! Esto significa que los stubs sólo son relevantes para frecuencias muy altas. ¡Pero usamos frecuencias muy altas en muchos de nuestros circuitos!
La primera frecuencia de notch a aquella en la que el retardo de la línea de transmisión del stub es igual un cuarto del periodo.
Podemos despreciar el efecto del stub para frecuencias inferiores a la mitad de la frecuencia del notch.
Hoy hemos hecho una aproximación en el dominio de la frecuencia, que da cierta visión de las magnitudes involucradas. Sin embargo, no es demasiado útil para una aplicación directa, para lo cual es más adecuado un análisis en el dominio del tiempo, pero esto es algo que abordaremos en el post de la próxima semana.
Para terminar recordaremos que
Hay stubs que son inevitables. Hay otros que son simples malas prácticas de diseño. Intentaremos domesticar los primeros y evitar los segundos.
La traducción de stub puede ser la de tocón: un trozo de tronco de árbol que sobresale de la tierra después de haber sido cortado un poco por encima del nivel del suelo. El sentido del humor de los padres de la electrónica era admirable.